Por Alberto Casanovas
Voy a hacer una pequeña introducción al mundo de la teoría musical. No es indispensable que os aprendáis todo lo que se va a explicar en este tutorial, sin embargo os puede ser de ayuda para entender ciertos conceptos musicales. Tampoco pretendo explicar solfeo ni como leer una partitura, probablemente deje muchas cosas en el tintero, y no profundice demasiado. Simplemente voy a intentar explicar lo que creo que os puede ser de utilidad en vuestras andaduras con el uke.
La música escrita podríamos considerarla una ciencia casi exacta, más cerca de las matemáticas que del arte. Obviamente la música va más allá de ciertos conceptos, reglas y partituras, pero comprender como funciona puede ayudar un poco a entender ciertas cosas.
En este tutorial voy a intentar explicar solo los conceptos más básicos, nomenclatura, formación de acordes y escalas básicas. Otro punto muy importante que vamos a tocar es la métrica, es decir tipos y duración de las notas, así como su agrupación en compases. Esto es tan importante como saber tocar un acorde (saber “llevar el ritmo” de una canción). Os advierto que es un tema un tanto espeso, no os agobiéis. ¿Preparados? Comencemos pues.
CONCEPTO DE TERCERA MAYOR Y TERCERA MENOR
RELACIÓN ENTRE TONALIDADES MAYORES Y MENORES
PROGRESIÓN ARMÓNICA DE UNA TONALIDAD
CIRCULO DE QUINTAS Y DE CUARTAS
NOMENCLATURA MUSICAL
Aunque estés empezando en esto, y el `ukulele sea tu primer instrumento, me imagino que sabrás que la música se compone de una sucesión de notas como si de letras que forman un texto se trataran. En la cultura occidental este “alfabeto” musical se compone de 12 notas. Si si, como lo oyes, desde J.S. Bach a Iron Maiden, todo se basa en 12 únicas notas.
Estas notas son las que podemos recitar de carrerilla gracias a Mary Poppins:
Do, Re, Mi, Fa, Sol, La, Si
Pero un momento – os preguntareis – ¿no dijiste 12 notas? Solo veo 7…
Efectivamente. Lo que Julie Andrews cantaba era realmente la escala mayor de Do, que se compone de 7 notas (como todas las escalas mayores, y muchas otras escalas). Estas siete notas se las conoce también como las notas naturales. Realmente, nos faltan una serie de notas entre medio de algunas de ellas. Son lo que conocemos como semitonos. Un semitono está en mitad de 2 notas consecutivas separadas por un tono (por ejemplo entre Do y Re), es decir que 2 semitonos forman un tono completo. Un semitono no lo podemos volver a dividir, nos encontramos ante la “partícula elemental” de la música (al menos de la música occidental).
Aplicado al piano, las teclas blancas están separadas un tono (verídico al 90%, ya veréis porque). Las teclas negras que quedan entre 2 teclas blancas son los semitonos. En una guitarra cada traste es un semitono, por tanto cada 2 trastes tenemos un tono completo. En el `ukulele ocurre de la misma forma.
Pongamos un ejemplo. Si tocamos la tercera cuerda del uke al aire sabemos que se trata de un Do (en afinación standard). Si pulsamos en el segundo traste, hemos avanzado 2 semitonos, o lo que es lo mismo, un tono completo, y por tanto según la cancioncilla de la señora Poppins, estaremos tocando un Re. Si avanzamos 2 trastes más, en el 4 traste tendremos un Mi… ¿fácil no? Vale, pues ahora vamos a rellenar los cinco huecos que faltan hasta llegar a las 12 notas que os dije.
Volvamos al piano, concretamente vamos a fijarnos en las teclas negras:

Podemos ver que entre algunas teclas blancas (tonos) no hay tecla negra (semitono). Es cierto, concretamente entre las notas Mi y Fa, y entre Si y Do no tenemos ningún semitono. Es por esto tenemos 12 notas (7 tonos y 5 semitonos) y no 14 notas (7 tonos y 7 semitonos). Por lo tanto, entre las notas Mi y Fa, y entre Si y Do siempre tendremos un semitono, directamente. Siempre, siempre. Palabra.
Pues muy bien diréis… y esos 5 semitonos ¿como se llaman? Bueno, esta pregunta es más complicada de lo que pueda parecer en un principio. Si fuésemos estrictos no podríamos decir su “nombre” a menos que sepamos la “escala”… Pero de momento, y para no liar más, voy a introducir los sostenidos (indicados con ♯) y los bemoles (indicados con ♭), conocidos en música como las alteraciones.
Un sostenido en una nota indica que debemos avanzar un semitono sobre la nota base. Es decir, la nota quedará alterada para que sea un semitono más aguda (en un piano significa avanzar hacia la derecha). Por ejemplo, un Do♯ será justo un semitono más agudo que un Do. En cambio un bemol indica que debemos bajar la nota un semitono, es decir, hacerla un semitono más grave (en el piano, hacia la izquierda). Por ejemplo, un Mi♭ es un semitono más grave que un Mi.
Así que ya podemos completar las 12 notas que componen nuestro “alfabeto“, teniendo en cuenta como hemos dicho que entre Mi y Fa ya están separadas un semitono con lo cual no podemos poder ningún sostenido en medio de las dos, igual que entre Si y Do. Para el ejemplo vamos a usar exclusivamente sostenidos:
Do Do♯ Re Re♯ Mi Fa Fa♯ Sol Sol♯ La La♯ Si
(la siguiente nota volvería a ser Do, una octava más agudo que el primero)
Si usamos únicamente bemoles:
Do Re♭ Re Mi♭ Mi Fa Sol♭ Sol La♭ La Si♭ Si
Comparando estas 2 “escalas” (la de “sostenidos” y la de “bemoles“), y a poco que seamos un poco avispados nos daremos cuenta que un sostenido y un bemol son la misma cosa, solo que tomando como referencia la nota anterior y subiéndola un semitono (los sostenidos) o cogiendo la nota superior y bajarla un semitono (los bemoles). Es decir, un Re♯ suena exactamente igual que un Mi♭ (es lo que se conoce como enarmonía). Os preguntareis ¿para que necesitamos 2 palabras para referirnos a la misma nota? Porque dependiendo de la armonía un sonido en concreto tendrá un nombre u otro. De momento quedaros con esto y con que en una misma escala o tonalidad (un conjunto de notas) nunca tendremos mezclados sostenidos con bemoles, ni la misma nota repetida (no podemos tener un La y un La♯).
Existen otras alteraciones a parte de los sostenidos y los bemoles. Se tratan de los becuadros, los doble sostenido y los doble bemol, etc. aunque por el momento, si no profundizáis más en teoría musical y armonía no los vais a necesitar para nada. Además existen otras alteraciones como los medios bemol, medio sostenido, bemol y medio, etc que son exclusivos de músicas no occidentales, en las que un semitono se puede dividir en partes más pequeñas.
NOMENCLATURA ANGLOSAJONA
Es sistema de notación anglosajón es exactamente idéntico al nuestro salvo en el nombre que tienen las notas naturales. A cada nota le dieron una letra del alfabeto de la A a la G, dando la primera letra a la nota La. Por tanto, la relación es la siguiente:
A = La
B = Si
C = Do
D = Re
E = Mi
F = Fa
G = Sol
Añadiendo las alteraciones ♯ y ♭ conseguimos los sostenidos (sharp en inglés) y los bemoles (flat en inglés) de la misma forma que con nuestro sistema.
Es importante que os aprendáis estos nombres alternativos ya que prácticamente la totalidad de información que encontréis por internet o en libros, estará anotada así. Yo suelo utilizar este sistema.
ESCALAS MAYORES
Antes de seguir, voy a introducir el concepto de escala. Una escala es un conjunto de notas diferentes que mantienen una cierta relación entre ellas. Dependiendo de esta relación, se determinará el nombre de la escala. La primera nota se la llama tónica o raíz. El resto de notas, llamados intervalos o grados, se les da un orden: segunda, tercera, cuarta, quinta, sexta, séptima (tendríamos la octava que es la misma nota que la tónica, una octava más aguda). Normalmente los intervalos se escriben en números romanos, por ejemplo si vemos V se refiere al quinto grado, que por ejemplo en la escala de C, se trata de G.
Una escala mayor es una sucesión de 7 notas separadas cada nota por un tono, excepto entre el tercer y cuarto grado, y entre el séptimo y el octavo (justo la misma nota que la tónica) que están separadas un semitono. Veámoslo con un ejemplo, la escala de C:
C D E F G A B (C)
Efectivamente entre el primer y el segundo grado (C y D) tenemos un tono (2 trastes), entre el segundo y el tercero (D y E) tenemos 1 tono, entre el tercero y el cuarto (E y F) un semitono (recordemos que entre E y F hay un semitono siempre), entre el cuarto y el quinto (F y G) hay un tono, entre el quinto y la sexto (G y A) un tono, entre el sexto y el séptimo (A y B) tenemos un tono, y entre el séptimo y el octavo (B y C, que vuelve a ser la tónica) tenemos un semitono (como ya sabemos, entre B y C hay un semitono siempre).
Para que nos acordemos. La estructura de una escala mayor siempre es tono-tono-semitono-tono-tono-tono-semitono, abreviado t-t-s-t-t-t-s (o en inglés whole-whole-half-whole-whole-whole-half, abreviado w-w-h-w-w-w-h).
Punto. Con esta teoría podemos montar cualquier escala mayor que queramos. Vamos a poner un ejemplo, la escala mayor de G. Pues siguiendo la teoría del w-w-h-w-w-w-h y empezando por la nota G que es la tónica, tenemos:
G A B C D E F♯ (G)
Efectivamente, entre todas las notas hay un tono excepto entre B y C (tercero y cuarto grado) y entre F♯ y G (séptimo y octavo). Nótese que me he visto obligado a utilizar una alteración (un sostenido) para poder fijar la distancia correcta entre la sexta y la séptima que debe ser de un tono. Curiosamente, esta alteración ha hecho que entre la séptima que hemos alterado y la octava haya la distancia correcta, un semitono. ¿Brujería? Ni mucho menos. Pongamos otro ejemplo, vamos a hacer la escala mayor de E, pero ahora la vamos a hacer por pasos siguiendo la regla del w-w-h-w-w-w-h.
Paso 1: poner el nombre de las 7 (8 si contamos la octava) notas de la escala, sin alteración ninguna, solo los nombres naturales. Como es la escala mayor de E, empezamos por esta.
E F G A B C D (E)
Paso 2: corregimos las distancias donde toque. Entre la primera y la segunda debe haber un tono completo, pero sabemos que entre E y F hay un semitono. Pues alteramos F a F♯ para que haya un tono entre el primer y segundo grado. Ahora la escala nos queda:
E F♯ G A B C D (E)
Pero debemos seguir. Ahora entre la segunda y la tercera hay un semitono, pero necesitamos un tono completo para que se cumpla la regla. Alteramos G a G♯ quedando:
E F♯ G♯ A B C D (E)
No hemos terminado, seguimos. Entre la tercera y la cuarta necesitamos un semitono. Premio! Entre G♯ y A ya hay un semitono, con lo cual lo dejamos como está.
Repetimos este proceso hasta comprobar todos los intervalos, y si lo hacemos bien obtendremos:
E F♯ G♯ A B C♯ D♯ (E)
Hemos obtenido la escala mayor de E que tiene 4 sostenidos.
Con este sistema podemos obtener cualquier escala mayor que se nos antoje. Si cogemos papel y lápiz e intentamos escribir la escala mayor de las 12 tonalidades obtendremos una secuencia de 7 notas distintas para cada tonalidad mayor! Nunca tendremos 2 secuencias iguales, todas las escalas mayores son distintas al menos en una nota ¿Impresionados?
De la misma forma que hemos escrito la escala usando sostenidos donde haga falta para tener los intervalos correctos, podemos utilizar bemoles. El sistema es el mismo. Técnicamente, solo se utilizan bemoles en las escalas mayores cuando la raíz o tónica de la escala es bemol, exceptuando la escala de F mayor que se escribe siempre con bemoles. En resumen:
- Si tónica no es bemol y no es F -> escala mayor con sostenidos
- Si la tónica es F o tiene un bemol -> escala mayor con bemoles
Vamos a poner un ejemplo. Queremos hacer la escala E♭ mayor. Como la tónica, en este caso E♭, es una nota alterada con un bemol, su escala mayor la haremos con bemoles, respetando siempre la regla de w-w-h-w-w-w-h:
E♭ F G A♭ B♭ C D (E♭)
Si comprobamos, se verifican los intervalos correctamente.
ESCALAS MENORES
Una escala menor (el nombre completo debería ser escala menor natural) es una escala en la que tenemos semitonos entre los intervalos 2º y 3º, y entre el 5º y el 6º. El resto de intervalos están separadas un tono completo. Siguiendo la regla que aplicamos para las escalas mayores, con whole y half, la escala menor sería w-h-w-w-h-w-w.
Pongamos un ejemplo. Vamos a escribir la escala de A menor natural. Ponemos las 7 notas empezando por A, y corregimos las distancias de los intervalos donde haga falta con sostenidos.
A B C D E F G (A)
Ha sido muy facil ¿verdad? Resulta que no hemos tenido que alterar ninguna nota. ¿No os suena de nada? Efectivamente, la escala de C mayor tampoco tiene ninguna alteración. Esto es porque estas 2 escalas, C mayor y A menor, en realidad son la misma cosa mirada con un prisma diferente.
Hagamos otro ejemplo, la escala de E menor.
E F♯ G A B C D (E)
Pues todas las escalas menores naturales se hacen de la misma forma, no tienen ningún secreto. Igual que con las escalas mayores, si cogéis papel y lápiz y hacéis las escalas menores naturales de las 12 tonalidades, obtendréis secuencias de notas diferentes en todos los casos.
CONCEPTO DE TERCERA MAYOR Y TERCERA MENOR
Una vez conocemos las escalas mayores y las escalas menores, vamos a definir qué es una tercera mayor y qué es una tercera menor.
Una tercera mayor es una nota que está a 2 tonos completos de la tónica (o 4 semitonos), tal como pasa en las escalas mayores. Es decir, se trata del tercer grado de la escala mayor. En la escala mayor de C, la tercera (un E) está justo a 2 tonos de C.
Una tercera menor es una nota que está a 1 tono y medio de la tónica (o 3 semitonos), como en una escala menor. O sea, es el tercer grado de la escala menor. Si tomamos el ejemplo de la escala menor de A, la tercera (un C) está justo a 1 tono y medio de A.
El intervalo de tercera es importantísimo en la formación de acordes que veremos más adelante.
RELACIÓN ENTRE TONALIDADES MAYORES Y MENORES
Cuando hablábamos de las escalas mayores y menores, vimos que una escala mayor X comparte las mismas notas con una escala menor Y. Esto es porque son tonalidades relativas, y comparten el número de alteraciones en su escala (número de sostenidos o de bemoles) y por lo tanto tienen las mismas notas. Toda escala mayor tiene su relativa menor (y a la inversa, claro)
El intervalo que separa una tonalidad relativa menor de su correspondiente tonalidad relativa mayor, siempre es de una tercera menor descendente, que como hemos visto, es un tono y medio.
Vamos a tomar de ejemplo las escalas de C mayor y la de A menor, que como sabemos comparten el número de alteraciones (concretamente, ninguna) y por lo tanto son relativas. Si descendemos un tono y medio partiendo de C, obtenemos justo un A:
C ← B ← A
De forma más directa, también podemos decir que la tonalidad menor relativa de una tonalidad mayor en concreto, se corresponde con el 6º grado de la escala mayor. Inversamente, podemos decir que la tonalidad mayor relativa de una escala menor en concreto, se corresponde con el 3º grado de la escala menor. Veamos un par de ejemplos.
Tenemos la escala mayor de G, con un sostenido:
G A B C D E F♯ (G)
Su sexto grado, E, es el relativo menor. Efectivamente, la escala de E menor solo tiene un sostenido:
E F♯ G A B C D (E)
Segundo ejemplo. Tomemos la escala de B menor:
B C♯ D E F♯ G A (B)
Como es una escala menor, nos fijamos en el tercer grado para obtener su relativo mayor, en este caso un D. Efectivamente, la escala mayor de D tiene 2 sostenidos.
Esto que es un auténtico tostón, son los cimientos de la música. Aunque, sin embargo, podamos vivir sin estos conocimientos básicos, y tocar un instrumento sin tener ni idea de como se forman los acordes, o porqué ese acorde en concreto es menor y no es mayor, etc… estas nociones nos pueden ayudar en el futuro a la hora de determinar los acordes de una canción o para componer las nuestras propias.
FORMACIÓN DE ACORDES
Un acorde no es más que la unión de 3 o más notas diferentes que suenan a la vez. Si la unión es de 3 notas, las llamamos tríada. Si pulsamos 3 teclas diferentes de un piano (diferentes quiere decir que no sean la misma nota, ni siquiera en una octava distinta) tendremos un acorde, no sabremos que nombre tiene, pero es un acorde.
Dependiendo de cómo formemos la tríada (concretamente el intervalo o número de semitonos que haya entre las notas que forman la tríada) tendremos un tipo de acorde u otro. En general, esto sirve para todos los acordes, tendremos una nota “base” la cual llamaremos “tónica” que es la que dará el nombre al acorde, y sobre la que se calcularan las distancias en semitonos del resto de notas de la tríada para determinar el tipo acorde. En resumen, tenemos 5 tipos de acorde básicos dependiendo de cómo formemos la tríada: mayores, menores, aumentados, disminuidos y suspendidos. De los 3 últimos de momento podéis olvidaros de ellos, con que sepáis que existen es suficiente. La formación de acordes mayores y menores si que debéis grabárosla a fuego. A medida que vayáis avanzando empezareis a incorporar en vuestro lenguaje los acordes suspendidos, luego los disminuidos, y los acordes aumentados en menor medida.
Acordes Mayores
Un acorde mayor se forma siempre con la tónica, una tercera mayor y una quinta justa. Una quinta justa es la nota que está a 3 tonos y medio de la tónica (o siete semitonos). Coinciden con los grados I, III y V de la escala mayor respectivamente. Podríamos decir también que un acorde mayor es una porción de la escala mayor, concretamente los grados I, III y V.
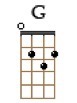
Pongamos un ejemplo. El acorde de G mayor (o GM o G a secas) se compone de G (tónica), B (tercera mayor a 2 tonos de la tónica, coincide con el III grado de la escala mayor de G) y D (quinta justa, a 3 tonos y medio de la tónica, coincide con el V grado de la escala mayor de G).
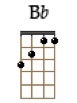
Otro ejemplo, el acorde de B♭ mayor se compone de B♭ (tónica), D (tercera mayor) y F (quinta justa). Comprobad las distancias.
Acordes menores
Un acorde menor se forma con la tónica, una tercera menor y una quinta justa, que coinciden con los grados I, III y V de la escala menor. Como veis, solo se diferencia de un acorde mayor en la tercera, que es menor (a un tono y medio de la tónica), a diferencia del acorde mayor donde es un intervalo de tercera mayor (a dos tonos de la tónica). Esta diferencia aparentemente inofensiva hace cambiar completamente el sonido del acorde y su carácter. Se suele indicar con una “m” minúscula al lado del acorde.
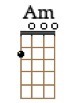
Un ejemplo, el acorde de Am, está formado por A (tónica), C (tercera menor, a un tono y medio de la tónica) y E (quinta justa, a 3 tonos y medio de la tónica).
Acordes aumentados
Un acorde aumentado se forma con la tónica, una tercera mayor y una quinta aumentada. Una quinta aumentada es un intervalo de 4 tonos respecto a la tónica. Viéndolo de otra manera, es superponer 2 intervalos de tercera mayor respecto a la tónica. Son un tipo de acorde inestable por si solo, crean cierta tensión. No se suelen utilizar demasiado. Se suele anotar añadiendo el signo “+” o “aug” detrás del acorde.
Un ejemplo, D+ (o Daug), estaría formado por D (tónica), F♯ (tercera mayor) y A♯ (quinta aumentada).
Acordes disminuidos
Un acorde disminuido se forma con la tónica, una tercera menor y una quinta disminuida. Una quinta disminuida es un intervalo de 3 tonos respecto a la tónica. Como vimos para los aumentados, también podemos entender los acordes disminuidos como la superposición de 2 intervalos de tercera menor. Igual que los aumentados, los acordes disminuidos crean mucha tensión. Los anotamos añadiendo el símbolo “º” o “dim” detrás del acorde.
Por ejemplo, el acorde de Dº (o Ddim), está formado por la D (tónica), F (tercera menor) y A♭ (quinta disminuida). Interesante ver que no hemos utilizado G♯ para indicar la quinta (aunque G♯ y A♭ serian notas enarmónicas), ya que el quinto grado de D es A. La nota G es el cuarto intervalo.
Acordes suspendidos
Hasta ahora todos los acordes que hemos visto tienen un intervalo de tercera, ya sea tercera mayor (acordes mayores y aumentados) o tercera menor (acordes menores y disminuidos). Un acorde suspendido es un acorde al cual hemos omitido el intervalo de tercera, sustituyendo el mismo por un intervalo de cuarta justa o por un intervalo de segunda mayor. Si utilizamos una cuarta justa (a 2 tonos y medio de la tónica) el acorde se llamará “sus4″. Si utilizamos una segunda mayor (a un tono de la tónica) el acorde se llamará “sus2″.
Son acordes que por si solos no funcionan, crean cierta tensión. La falta de tercera deja estos acordes un poco indeterminados, no son ni mayores ni menores. Además los intervalos de segunda mayor y cuarta justa crean cierta disonancia en el acorde.
Pongamos un par de ejemplos. El acorde Dsus2 está formado por D (tónica), E (segunda mayor) y A (quinta justa). El acorde Dsus4 está formado por D (tónica), G (cuarta justa) y A (quinta justa).
CUATRÍADAS
Vamos a hacer una breve introducción al concepto de acorde de cuatríada. Una cuatríada es una acorde formado por 4 notas, y se construye añadiendo un intervalo de séptima a una tríada. Hay varios tipos de cuatríada, pero vamos a centrarnos únicamente en 2. Trataremos únicamente tríadas mayores a las cuales les añadimos una séptima mayor o una séptima menor, las más usuales.
Si a un acorde mayor le añadimos un intervalo de séptima mayor (5 tonos y medio), obtenemos un acorde mayor séptima. Lo anotamos añadiendo “maj7″ detrás. Si le añadimos un intervalo de séptima menor (5 tonos) obtenemos un acorde de séptima o habitualmente conocidos como séptima dominante o dominante a secas. Lo anotamos añadiendo “7″ detrás del acorde.
PROGRESIÓN ARMÓNICA DE UNA TONALIDAD
La progresión armónica de una tonalidad es una sucesión de acordes concordantes con cada grado de la escala. En pocas palabras, cada intervalo o grado de una escala tiene asociado un acorde. Vamos a estudiar las progresiones armónicas de una tonalidad mayor y de una menor.
Vamos a partir de una escala mayor, por ejemplo la de C:
C D E F G A B
A cada intervalo le asignamos un acorde, tal como sigue:
I -> acorde mayor -> C
II -> acorde menor -> Dm
III -> acorde menor -> Em
IV -> acorde mayor -> F
V -> acorde mayor -> G
VI -> acorde menor -> Am
VII -> acorde semidisminuido -> Bm7b5 (olvidaros de él)
Bien, pues si estamos en la tonalidad de C, cualquiera de esos acordes funcionarían bien (unos mejor que otros), pero siempre estaríamos tocando dentro de la armonía. Si por ejemplo se nos ocurre tocar un F♯m o un E enseguida veremos que algo no cuadra, nuestro oído nos alertará que algo no funciona.
Si cogemos el sexto grado de una escala mayor sabemos que obtenemos el relativo menor, en este caso Am. Pues si reordenamos, obtendremos los acordes de la tonalidad de Am.
Para vuestras aspiraciones iniciales simplemente debéis saber que hay acordes más importantes que otros a parte del acorde de la tónica obviamente. Estos acordes son el IV (llamado subdominante) y el V (llamado dominante). Comprobareis que muchísimas canciones se basan en estos acordes, tónica, subdominante y dominante. En una tonalidad mayor estos 3 acordes son mayores. En una tonalidad menor estos 3 acordes son menores.
Podemos enriquecer nuestra progresión de acordes utilizando cuatríadas en vez de tríadas. En ese caso la progresión quedaría así (seguimos en la tonalidad de C mayor):
I -> Cmaj7
II -> Dm7
III -> Em7
IV -> Fmaj7
V -> G7
VI -> Am7
VII -> Bm7b5
CÍRCULO DE QUINTAS Y DE CUARTAS
El círculo de quintas es una representación de la relación de los 12 tonos que tenemos en la música occidental, así como las alteraciones que tiene cada todo. Se representa como un círculo donde, a modo de reloj, se va poniendo un tono donde le correspondería una hora en el reloj, ocupando la tonalidad C las “doce” de un reloj. Cada tono está separado del anterior, siguiendo el sentido de las agujas del reloj, en un intervalo de quinta. Si avanzamos en sentido contrario a las agujas del reloj, el intervalo es de cuarta.
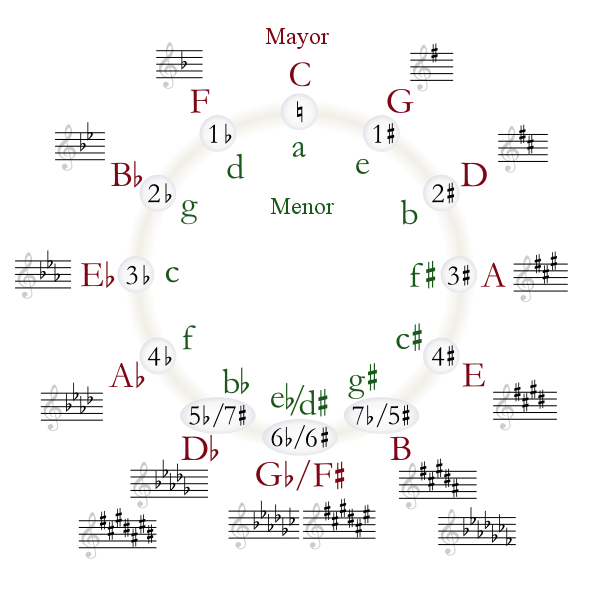
Curiosamente este tipo de representación permite ordenar las distintas tonalidades de forma que vayan aumentando en número de alteraciones. Si avanzamos por quintas (sentido de las agujas del reloj) vamos aumentando el número de sostenidos. Si lo comprobáis en la imagen anterior, C no tiene alteraciones, G tiene un sostenido, D tiene 2 sostenidos… hasta llegar a F♯ que tiene 6 sostenidos.
En cambio, si avanzamos por cuartas (girando en sentido contrario a las agujas de un reloj) vamos aumentando el número de bemoles. Como sabemos C no tiene alteraciones. F tiene un bemol, Si♭ tiene 2 bemoles… hasta llegar a Sol♭ que tiene 6 bemoles. Lo podéis comprobar en la imagen.
Esto, que aparentemente es una simple curiosidad, es de gran utilidad a la hora de determinar el número de alteraciones de una tonalidad, y por ende, sus escalas mayor y menor, y los acordes que derivan. Aprenderos este “truco” de memoria y sereis capaces de obtener los acordes de una tonalidad en cuestión de segundos ¡y sin tener que contar intervalos!
Para ello nos vamos a aprender el circulo de quintas empezando por el F (en vez de por el C) y sabiendo que F tiene un bemol y C no tiene ninguna alteración. Es lo único que os debéis aprender.
F C G D A E B
1♭ ♮ 1♯ 2♯ 3♯ 4♯ 5♯
Pues según este orden, sabemos que F tiene un bemol, C no tiene alteraciones, G tiene un sostenido, D tiene 2 sostenidos, A tiene 3 sostenidos, E tiene 4 sostenidos, y por último, la tonalidad de B que tiene 5 sostenidos. Bien, imaginemos que queremos determinar la escala mayor de A. Sabemos que tiene 3 sostenidos. ¿Cuales serán estas notas sostenidas? Pues las 3 primeras de nuestro circulo de quintas que nos acabamos de aprender, es decir, F, C y G. Esas 3 notas serán sostenidos, el resto naturales. Veamos si cuadra:
A B C♯ D E F♯ G♯
¡Pues cuadran los intervalos! Será casualidad, vamos a probar la escala mayor de D. Sabemos que la tonalidad de D tiene 2 sostenidos, que deberían ser F y C. Comprobémoslo:
D E F♯ G A B C♯
¡También cuadran! ¿Increíble no?
¿Y qué pasa con las tonalidades que no tenemos en nuestro circulo de quintas? Vamos a poner un ejemplo, vamos a intentar sacar las notas de la tonalidad de G♯. Pues muy sencillo, partimos de la escala sin alterar, en este caso G, y aumentamos todo medio tono. Sabemos que la escala de G tiene un sostenido (F♯):
G A B C D E F♯
Aumentamos todo medio tono:
G♯ A♯ B♯ C♯ D♯ E♯ F♯♯
Siempre hay que respetar la nota en cada intervalo. Aunque sepamos que B♯ realmente es un C, en la escala debemos mantener el B♯. Igual que F♯♯ es un G, debemos mantener el F en el séptimo grado.
Si lo que queremos saber es las notas de una escala con bemoles (es decir la escala de F o cualquiera que la tónica sea bemol), usaremos el circulo de cuartas (en el sentido contrario a las agujas del reloj), y debemos seguir este orden.
B♭ E♭ A♭ D♭ G♭ F
2♭ 3♭ 4♭ 5♭ 6♭ 1♭
Funciona de forma parecida que con los sostenidos, salvo que empezamos con B♭ que tiene 2 bemoles, y terminamos con G♭ que tiene 6 bemoles y la excepción que es F, que como sabemos, tiene 1 bemol. Si queremos determinar la notas de la tonalidad de A♭, sabemos por el círculo de cuartas que A♭ tiene 4 bemoles:
A♭ B♭ C D♭ E♭ F G
Con este sencillo método podemos saber en un santiamén las notas de una escala, y de ahí los acordes de la progresión armónica. Experimentad un poco y veréis que es muy sencillo.
METRICA MUSICAL
Hasta ahora hemos estado viendo que la música se compone de notas, que se relacionan entre si, que se agrupan para formar acordes, etc.
Pero la música no solo es una sucesión de notas. La música es ritmo. Una misma ristra de notas suenan totalmente distintas dependiendo del ritmo con que las toquemos. Vamos a introducir el concepto de compás, de tempo, y conoceremos las distintas figuras musicales.
Compás
El compás o métrica es una entidad musical que nos dice como se subdivide la música. En una partitura lo veremos al principio del pentagrama, expresado normalmente como una fracción. Si durante el transcurso de la canción se modifica la métrica, se indica poniendo el valor del nuevo compás. El compás nos permite dividir la partitura en compases. Las barras de compás es cada una de las subdivisiones que hacemos de una partitura, indicado mediante unas líneas verticales.
Rítmicamente, cada compás tiene la misma duración, o dicho de otra forma, en cada compás cabe el mismo número de figuras musicales (aunque como veremos, no todas las figuras duran lo mismo).
Como he comentado, el compás se indica mediante una fracción. El numerador de la fracción (el número de arriba) nos indica en cuantas partes se dividirá cada compás, es decir nos indica cuantos pulsos o tiempos tendrá nuestro compás. El denominador (el número de abajo) nos indicará la unidad de tiempo o figura que llenará cada tiempo del compás siguiendo esta tabla (más adelante os explicaré cada figura, no os preocupéis):
1 → redonda
2 → blanca
4 → negra
8 → corchea
16 → semicorchea
(hay subdivisiones más pequeñas, como la fusa, semifusa o garrapatea, de las que no entraré en detalle debido a su poco uso).
Ahora ya sabemos que quiere decir la fracción con la que se representa un compás. Veamos unos ejemplos:
4/4
El numerador nos indica que este compás se divide en 4 tiempos o pulsos. El denominador nos indica que cada tempo es una figura negra. Dicho de otra forma, en cada compás tendremos 4 figuras negras, una por cada tiempo del compás. Este es el compás más utilizado en la música contemporánea (pop, rock, blues, etc).
2/4
El numerador nos indica que se divide en 2 pulsos, y el denominador nos dice que serán negras. Es decir, cada compás tendrá 2 figuras negras.
Intentad descifrar que querrá decir un compás 3/4 y un compás 12/8.
Un apunte importante. Como sabemos el denominador nos dice la figura que rellena cada pulso del compás, y sabemos cuantos pulsos tiene por el numerador. Eso no quiere decir que un compás 4/4 siempre tenga 4 negras, una en cada pulso del compás. La métrica nos dice la duración total del compás, pero nosotros podemos utilizar tantas figuras musicales como queramos mientras no superemos la duración marcada por el compás. La duración de cada figura es siempre la mitad que la anterior siguiendo la lista que vimos antes. Es decir, una blanca dura la mitad que una redonda, una negra dura la mitad que una blanca (o la mitad de la mitad de una redonda, es decir un cuarto), una corchea dura la mitad que una negra (o un octavo de una redonda), y una semicorchea dura la mitad que una corchea (o una decimosexta parte de una redonda). Lo vemos con un ejemplo.
Un compás 4/4 lo podemos rellenar con:
- Una redonda (ocupará los 4 pulsos del compás)
- Dos blancas (una ocupará los 2 primeros pulsos, la segunda el resto)
- Cuatro negras (tal como vimos)
- Ocho corcheas (tendremos dos corcheas por cada pulso)
- Dieciséis semicorcheas (cuatro semicorcheas por pulso)
Además podemos combinarlo de cualquier forma siempre y cuando la suma total sea de 4 negras.
- Una blanca y 2 negras
- Una negra, 2 corcheas, y 8 semicorcheas
- 8 corcheas
- …
Podemos combinarlas como queramos.
Figuras musicales
Aunque prácticamente ya las hemos visto, vamos a ver su representación y duración.
Redonda o whole note
La redonda se representa con la figura ![]() y se trata de la figura con más duración. Ocupa un compás 4/4 al completo.
y se trata de la figura con más duración. Ocupa un compás 4/4 al completo.
Blanca o half note
La blanca se representa con la figura ![]() y su duración es la mitad de una redonda. Ocupa medio compás 4/4.
y su duración es la mitad de una redonda. Ocupa medio compás 4/4.
Negra o quarter note
La negra se representa con la figura ![]() y su duración es la mitad de una blanca, o un cuarto de una redonda. Ocupa un cuarto de compás 4/4.
y su duración es la mitad de una blanca, o un cuarto de una redonda. Ocupa un cuarto de compás 4/4.
Corchea o eighth note
La corchea se representa con la figura ![]() y su duración es la mitad de una negra, o un octavo de una redonda. Ocupa una octava parte de compás 4/4, es decir “caben” 2 corcheas en cada pulso del compás.
y su duración es la mitad de una negra, o un octavo de una redonda. Ocupa una octava parte de compás 4/4, es decir “caben” 2 corcheas en cada pulso del compás.
Semicorchea o sixteenth note
La semicorchea se representa con la figura ![]() y su duración es la mitad de una corchea, o una decimosexta parte de una redonda. Ocupa una decimosexta parte de compás 4/4, es decir “caben” 4 semicorcheas en cada pulso del compás.
y su duración es la mitad de una corchea, o una decimosexta parte de una redonda. Ocupa una decimosexta parte de compás 4/4, es decir “caben” 4 semicorcheas en cada pulso del compás.
Puntillo
El puntillo es un signo musical que indica que la nota a la cual acompaña se prolonga su duración la mitad de la misma. Por ejemplo una blanca con puntillo dura 3 tiempos (en un compás 4/4), lo que equivaldria a 3 negras. Una negra con puntillo dura 1 tiempo y medio, lo que equivaldria a 3 corcheas.
Se indica con un punto a la derecha de la nota afectada.
Silencios
Cada figura musical lleva asociada una figura de silencio. Como su propio nombre indica, no es más que un silencio (no tocamos nada) durante la duración de la figura que representa. Es decir, un silencio de negra implica no tocar durante la duración de una negra.
Tempo
Hasta ahora hemos visto como se subdivide la música en compases, todos de la misma duración. Pero no hemos hablado de cuanto dura realmente cada compás. Ahí entra el concepto de tempo.
El tempo se mide en pulsos por minuto, en inglés beats per minute abreviado bpm. Como vimos, un compás se divide en pulsos o tiempos. Pues el tempo nos dice cuantos tiempos habrá en un minuto, tan sencillo como eso.
El tempo se indica al principio de la canción, y cada vez que haya un cambio del mismo.
Con la ayuda de un metrónomo, podemos ir siguiendo el ritmo y marcando la duración de las notas. Basándonos en el compás y el tempo, regularemos el metrónomo. Por ejemplo, tenemos un compás 4/4 y el tempo nos indica que es a 60bpm. Es decir, tenemos 60 tiempos en un minuto. En un compás 4/4, como ya sabemos, cada tiempo es una negra, con lo cual tocaremos 60 negras en un minuto, es decir una cada segundo. Todas duraran exáctamente lo mismo. En este caso, regularíamos el metrónomo a 60bpm y tocariamos una negra coincidiendo con cada click del metrónomo.
De la misma forma, podríamos tocar a corcheas esto sería tocar 2 notas por cada click del metrónomo (recordemos que una negra son dos corcheas), y en total tocaríamos 120 notas en un minuto.
Y así con el resto de figuras. Una redonda serían 4 clicks; una blanca 2 clicks; 4 semicorcheas en un click.
Si tenéis un metrónomo, utilizadlo. Si no tenéis, ¡os compráis uno! (o utilizad un metrónomo online, o una aplicación para smartphone). Es importante que os acostumbréis a tocar a tempo, y que seais capaces de hacer las subdivisiones necesarias de forma precisa. Es decir, si el metrónomo marca negras en cada click, seais capaces de tocar corcheas y semicorcheas sin problema en medio de cada click.
De la misma forma que os estoy diciendo que aprendáis a usar el metrónomo, y ser capaces de tocar a tempo, os digo lo contrario. Hay que ser un poco flexibles, alargar ciertas notas, acortar otras… acompañado de ciertas técnicas como puede ser el vibrato, los ligados… en conjunto harán nuestra interpretación única (feeling). Siempre de forma controlada.
Patrones rítmicos
Las figuras musicales que hemos visto, a parte de indicar la duración de la nota, nos indican de qué nota se trata según su posición en el pentagrama. Para representar un rítmo se utiliza el mismo principio que para las figuras musicales salvo que no es necesario indicar una nota, con la duración tenemos suficiente. Lo simplificamos al máximo. De esta forma se transcribe la percusión y los patrones rítmicos.
Para indicar un ritmo usaremos los rhythm slashes que vienen a ser figuras musicales simplificadas. Tenemos rhythm slashes de redonda, de blanca, de negra, etc. Aquí los vemos:
Los patrones rítmicos se pueden agrupar como queramos siempre respetando la duración del compás tal como hacemos con las figuras musicales normales. Además las podemos prolongar con un puntillo si es necesario.
Pongamos un ejemplo de un patrón rítmico en un compás 4/4:
Pongamos el metrónomo a 60bpm o la velocidad que estéis cómodos. Cada click es una negra. Por lo tanto en el primer click tocaremos una negra, en el segundo click deberemos tocar las dos corcheas (la primera coincidirá con el click, y la segunda justo entre los clicks segundo y tercero), cada una durará medio tiempo, deben tener la misma duración. En el tercer click tocaremos otra negra. En el cuarto click tocaremos dos corcheas (la primera coincidirá con el click, y la segunda justo entre los clicks cuarto y primero del siguiente compás).
Cuando era pequeño me lo enseñaron así, por si os ayuda. La sílaba TA dura un tiempo. La sílaba TI dura medio tiempo, y la sílaba RI un cuarto de tiempo. Se corresponden con negra, corchea y semicorchea respectivamente. El ejemplo sería TA – TI TI – TA – TI TI
¿Lo veis?
Y hasta aquí nuestra introducción a la teoría musical. Espero que no se os haya atragantado mucho y os sea de utilidad.













































































































































































































































































































































































































































































































































 Una
Una 






[...] todas las pentatónicas, se compone de 5 notas. La forma de obtener las notas es partir de la escala menor natural de la tonalidad, y eliminar el segundo y el sexto [...]
[...] sucesivamente las 5ª justas (es decir, 3 tonos y medio) hasta obtener 5 notas (podéis utilizar el círculo de quintas). Al final, la sucesión de notas que obtengamos, las ordenamos dentro de la octava (de grave a [...]
https://ukulelespain.com/rincon-del-novato/teoria-musical#metrica